CMU Buggy Sim
October 2023 - December 2023
- Tech Stack: Python, Webots
- Summary
Deployed and tuned a PID controller for a Tesla Model 3, using Webots and Python.
Modeled the system as a Kinematic Bicycle Model, and analyzed its controllability and stability.
Compared numerical optimization methods like LQR and MPC, while integrating an A* planner and EKF-SLAM framework achieving a maximum cross-track error of 4m.
My role: Implemented everything, as it was a solo project.
- In-Depth
Introduction
This project was completed as part of the Modern Control Theory (24-677) course at CMU. Various control techniques and algorithms were implemented by applying them in a simulation of the CMU tradition of Buggy race. Various algorithms like PID, LQR, MPC A* and EKF SLAM were applied by ensuring the desired performance criteria.Motivation
The aim was to learn various control techniques and algorithms by applying them in a simulation of the CMU tradition of Buggy race. This would also help students participating in the Buggy race that is held annualy, as the track and data match the actual race.Methodology
For the purposes of the sim, I modeled a Tesla Model 3 using the Kinematic Bicycle Model. The first step was to start with the simplest controller - the PID (Proportional Integral Derivative) controller. Next, I delved into the realm of Optimal Control and implemented the LQR (Linear Quadratic Regulator) using Riccati recursion and Model Predictive Control (MPC) using Convex Trajectory Optimization, and compared it with the PID implementation. The next step was to implement an A* planner to overtake another car that was on the track. Finally, since in all the methods above we assumed that we had perfect measurements of the state, we implemented EKF-SLAM (Extended Kalman Filter SLAM) to account for uncertainty in the state estimate.
- Results
With PID, the time taken to complete the track was 243.776 s.
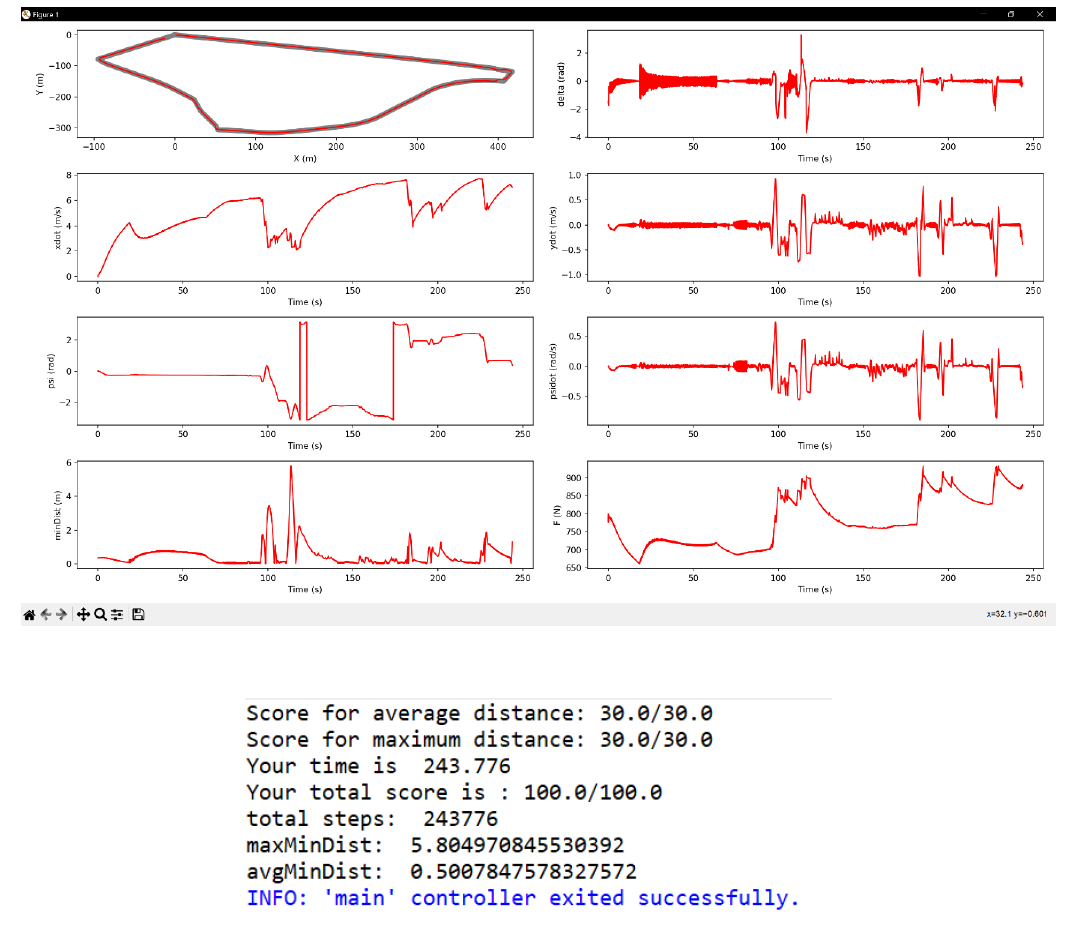
Fig-1 Performance plots of the PID Controller With LQR, the time taken to complete the track was 152.96 s. Hence, it was significantly faster than the PID.
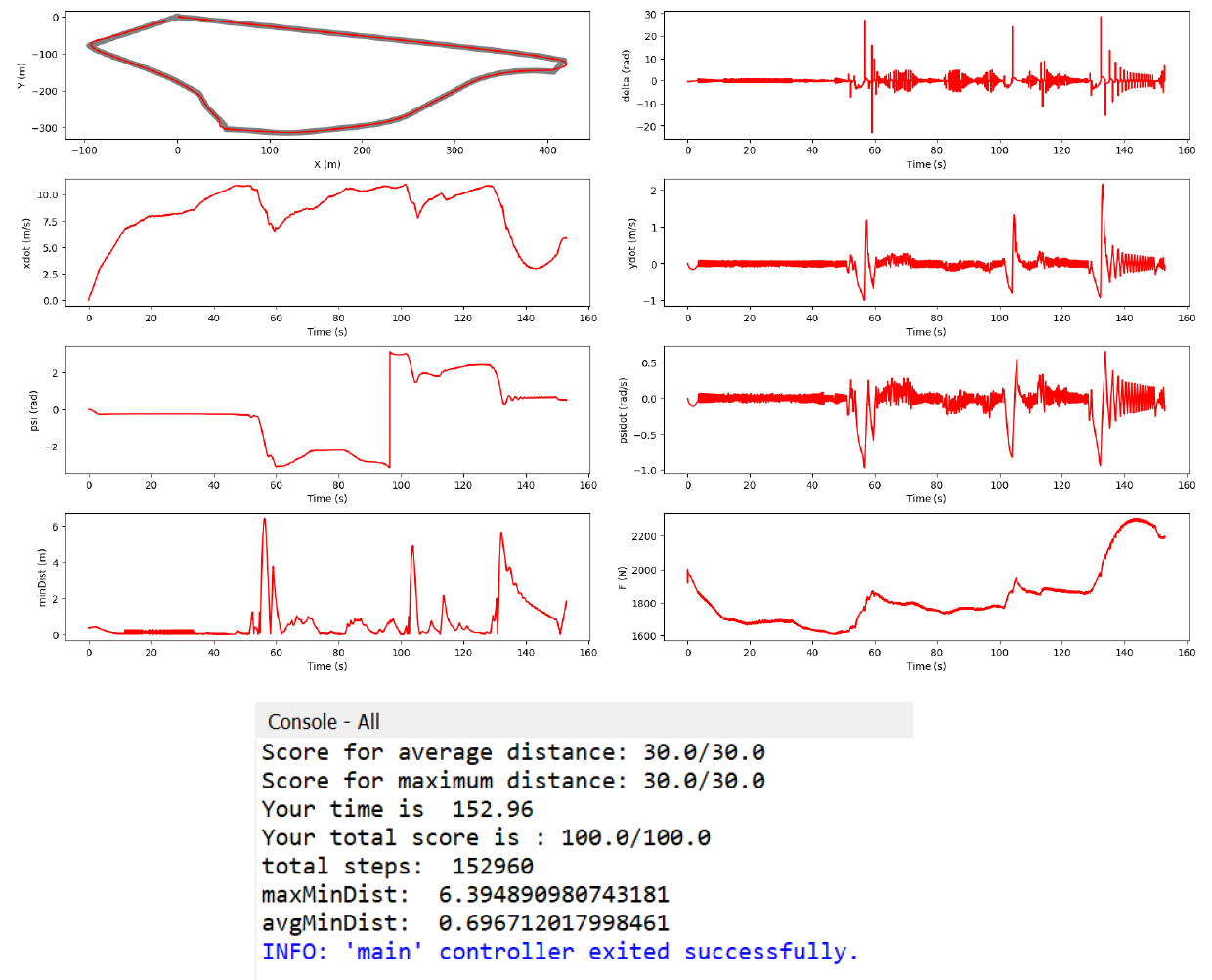
Fig-2 Performance plots of the LQR Controller EKF-SLAM was integrated with the LQR controller implemented previously, to get a track completion time of 158.368 s.
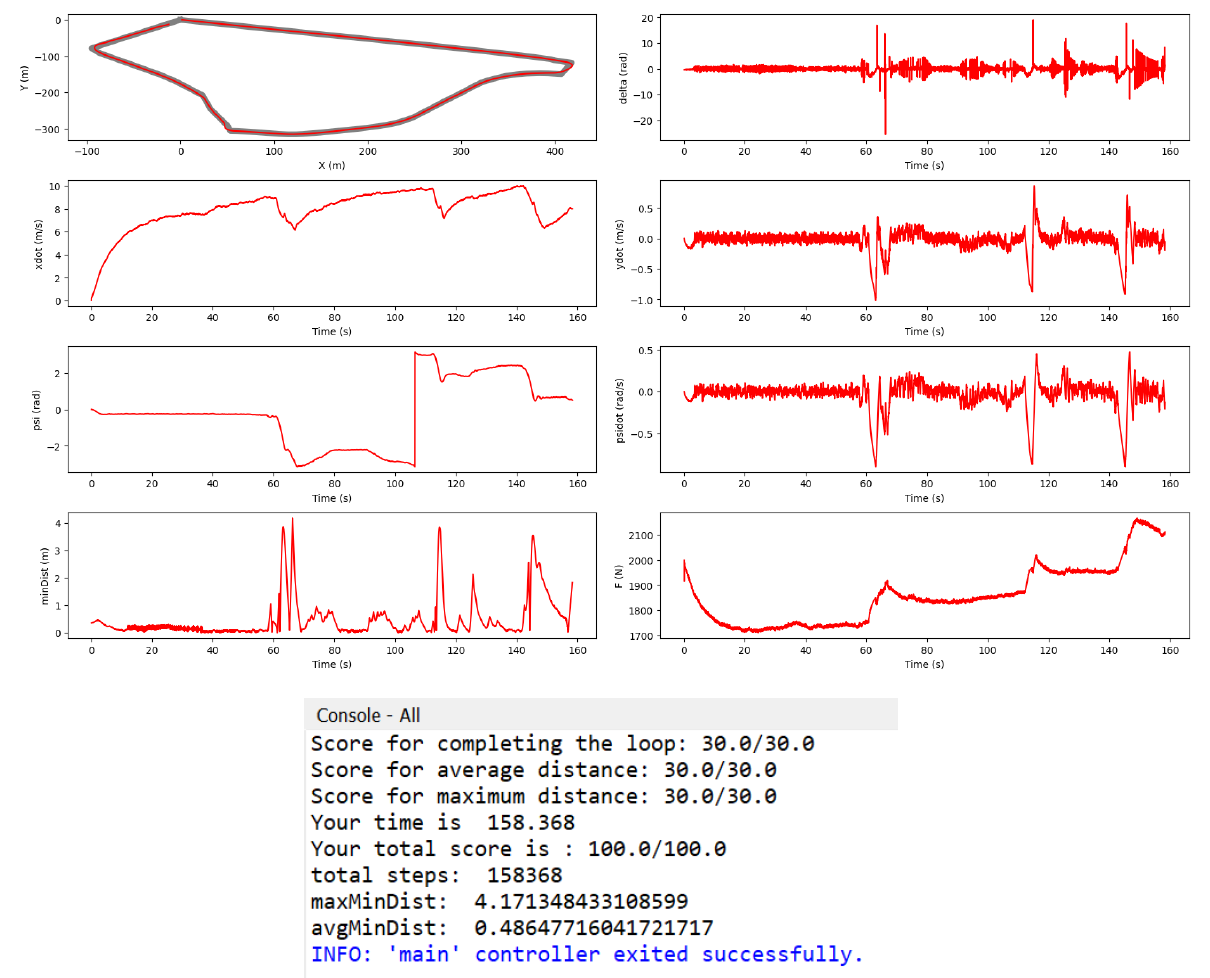
Fig-3 Performance plots with EKF-SLAM
